Git

I know the git has version rollback function, but I didn’t care too much before, because I think I’ve already uploaded my file to github, if I just want the previous version back why not just download the file back from GitHub? And I always think that git pull can do this for me, but I was wrong, if I modified the file and ran with git pull, it doesn’t work.

Well, it is time to pay for my lazyness, I finally met this stupid situation, I messed it up and all I wanted is to get my previous file version back. Git reset saves me.

You can use git log to view the commit history, Head indicates your current version, and use git reset --hard commit_id to get back to the past. Or you can use git reflog to view the command history and to jump to the future.

non-parametric fit

刚看到这种说法的原句是top 3000 high variable genes were selected on the basis of a non-parametric fit of the coefficient of variation using the mean as predictor(using support vector regression)，刚看完有点懵逼，去了解一下统计学上的非参数的含义，一是说不需要假定数据属于任何特定的分布，二是不对模型的结构做固定的假设。通常包括两种：一种是非参数的回归，对变量之间的关系结构做非参数化的建模，但模型的残差分布可能存在参数化的假设（因为是非参模型是考虑排序信息）。并不是说模型完全没有参数，而是说参数的维度是灵活可变的，存在于无穷维空间内（用泛函来分析）。

SVM，KNN和高斯过程回归都是非参模型。以高斯过程回归为例，这是一个非参数统计模型，也就是说即使我们通过学习得到了均值和高斯核的参数，模型仍然不能被唯一确定，参数的数量会随着模型复杂度的增长而改变，所以在参数模型中可以通过参数估计的方法去做预测，但非参模型中一般用蒙特卡洛方法进行纯数值的预测。

高斯过程

全称是高斯分布的随机过程（与时间有关的随机变量），任意一个点x，对应一个高斯随机变量f(x)，联合概率也可以简写成高斯分布，均值假设为0，还有一个核函数K。联合概率看作先验，观测y作为后验，然后在新的点上做预测。

一般假设噪声服从标准正态分布。

贝叶斯最优化

还是针对上面的高斯过程，可以加入贝叶斯的思想，通过从先验中抽取样本更新后验来近似真实后验。

有几个重要的概念，一个是prior先验概率，这个求起来很简单，就是一大堆数据中求某一类数据占的百分比就可以了，比如300个一堆的数据中A类数据占100个，那么A的先验概率就是1/3。第二个就是likelihood，likelihood可以这么理解：对于每一类的训练数据，我们都用一个多变量的正态分布来拟合它们(即通过求得某一分类训练数据的平均值和协方差矩阵来拟合出一个正态分布)，然后当进入一个新的测试数据之后，就分别求取这个数据点在每个类别的正态分布中的大小，然后用这个值乘以原先的prior便是所要求得的后验概率post了。

贝叶斯公式中还有一个叫evidence，实则上，evidence只是一个让最后post归一化的东西，而在模式分类中，我们只需要比较不同类别间post的大小，归一化反而增加了它的运算量。当然，在有的地方，这个evidence绝对不能省，比如GMM中，需要用到EM迭代，这时候如果不用evidence将post归一化，后果就会很可怕

GMM（高斯混合模型）

和贝叶斯分类器的不同在于，贝叶斯分类器的训练集是有分类信息的，我们可以直接求均值和协方差来拟合一个正态分布。但GMM对这些一无所知，所以在运算时不仅需要估算每个数据的分类，还要估算这些估算后数据分类的均值和协方差矩阵，用到的方法叫EM，具体方法就不在这里展开了。

Kaggle

成立于2010年，是一个进行数据发掘和预测竞赛的在线平台，可以独立做一下101和playground的训练赛来熟悉入门：这里有一个非常好的资源集成博客，如果大家有兴趣可以深入了解一下。

蒙特卡洛方法

用于解决多维，不连续问题的方法。

比如在积分问题无法找到原函数的情况下，可以通过用一个随机变量对被积函数进行采样的方法来求解，采样可以是均匀的也可以是不均匀的。数学上可以证明随着采样点的增多，求解是收敛的。

大致的思路是通过生成大量的随机数，给出一个参数的近似值。

看起来很像随机投点，但实际上是不同的，随机投点在一维上还可以做，但当维度升高的时候会有维度灾难，点在空间的分布会变得非常稀疏。但蒙特卡洛方法并不会受到影响，这是由它的一些特殊的处理方法决定的。比如采样点的选择（逆变换采样，拒绝采样，Metropolis method），方差缩减（解析积分-均匀样本放置，自适应样本放置）等等。

蒙特卡洛树搜索

在强化学习中好像比较重要，棋类游戏的模拟中也会用到，大致分成四步：选择(Selection)，拓展(Expansion)，模拟(Simulation)，反向传播(Backpropagation)

搜索树中的每一个节点包含了三个基本信息：代表的局面，被访问的次数，累计评分。UCT (UCB for Tree)是最经典的代表算法。

马尔可夫链

马尔可夫链由概率相互关联的序列组成，每一事件来自一组结果，每个结果根据一组固定的概率确定下一个结果。马尔可夫链的命名者安德烈·马尔科夫（Andrey Markov）最著名的案例之一就是要从一部俄罗斯诗歌作品中输出数千个“两字母对”（two-character pairs）。利用这些对，他计算了每一字母的条件概率。也就是说，给定前面的字母或空格，就能预测下一个字母是A还是T，或是一个空格。利用这些概率，马尔可夫可以模拟任意长的字符序列，这就是马尔可夫链。尽管前几个字母很大程度上取决于起始字母的选择，但是马尔可夫表明，从长远看来，字母的分布也遵循一种模式。因此，即使是相互依赖的事件，如果它们受到固定概率的影响，也将遵循平均水平的模式。

马尔可夫链蒙特卡洛方法（MCMC）

MCMC方法是用来在概率空间，通过随机采样估算兴趣参数的后验分布。

在贝叶斯统计中，代表参数信念的分布被称为先验分布。可能性分布通过表示参数值的范围和每个参数所体现的正观察数据的可能性，总结了已观测数据的意义。然后我们要做的是结合上述两个分布，去估计后验分布，在前两个分布非常标准的情况下可以直接求解，在遇到困难的时候，就可以用MCMC方法。

MCMC方法是蒙特卡洛方法的一种更通用的形式。其中有一个很关键步骤叫做细致平稳条件，为了解决采样的问题，有MCMC采样，M-H采样，Gibbs采样，现在Gibbs采样用的是最多的，有了Gibbs采样来获取概率分布的样本集，有了蒙特卡罗方法来用样本集模拟求和，他们一起就奠定了MCMC算法在大数据时代高维数据模拟求和时的作用。

Kinetic Monte Carlo

又称Gillespie算法。是一种通过蒙特卡洛抽样模拟化学体系随动力学行为的算法。

虽然Gibbs算法使得提议的接受率为1，让算法的效率更高并且在高维应用更稳定，但其对提议分布和目标分布的要求太过苛刻，大部分时候还是需要用Metropolis-Hasting算法。而接受率的出现使得部分提议无法接受，让算法的计算量增加，并且在高维时又因为各维度接受率的存在而使得提议效率急剧降低。如何提出不需要接受率的方法就成了一件比较重要的工作。

依然延袭MCMC的大框架，但对Metropolis-Hasting算法中每步都考虑是否接受进行改进，提议一定接受，并计算接受该提议所需要的时间。有很大一部分系统的概率演化都可以表示成ODE的形式，被称为主方程或者Fokker-Planck方程（Kolmogorov方程的直接推论 ）。Fokker-Planck方程称为化学中的质量守恒方程，浓度具有概率意义，里面的Q也具有概率意义，更深地牵扯到一些物理，化学，数学的东西，就实在有些复杂了。用该算法可以解这种方程里的Q矩阵。

朗之万方程

这个牵扯到的东西就非常理论物理了，从统计力学的哈密顿系统开始建立一个完全确定的动力系统，刚开始是用于研究溶液/大分子胶体/悬浮液系统的。从中可以积分得到溶剂分子的轨迹，经过一系列变换可以转变为一个非确定的，带高斯白噪声的随机微分方程，这就是朗之万方程。然后通过布朗运动满足的一些性质来进行修正，给朗之万方程一个更加严谨的定义，它有两种形式，一种是伊藤-朗之万积分，一种是Stratonovich-朗之万积分。通常选用保持“因果律”的伊藤公式，为了计算，后续要需要对其进行链式法则的修正。

换个思路，还是从随机微分方程出发，它描述的是某个流体中悬浮着的粒子的轨迹，限定在马尔可夫过程中，经过推导可以得到Chapman-Komogorov方程。马尔可夫过程的概率密度随时间的增量等于这段时间内流入这一区域的概率，减去流出这一区域的概率，由此我们可以写出主方程，由朗之万方程对应的马尔可夫过程的主方程又叫做Fokker-Plank equation，这个方程也有对应的两种诠释（Stratonovich积分和伊藤积分），FP方程实际上就是概率密度的扩散-漂移方程。ps. 类似地，与反向主方程类似，我们也可以得到反向FP方程。

FP方程所描述的系统，可以对稳态的细致平衡条件（detailed balance condition）作出讨论，也就是说稳态的一定时间t’-t内，观察到从相空间中的一个点到另一个点的概率， 等于其逆过程的概率。

路径积分的构造：根据CK方程，写出维那过程（因为布朗运动更为严谨的数学定义又维那给出，所以又称为维那过程）的概率密度函数，化出泛函形式，把一般的朗之万方程代入，就得到了概率幅的路径积分构造，此时再考虑粒子走某条路径的概率，就有了大偏差定理的形式。

求解的时候需要用到平均场近似，等等一系列条件分析，不再深究。

机器学习的一般过程

数据收集-数据预处理-模型训练-模型评估-可视化

数据预处理阶段可能遇到的问题有：数据缺失，离群点，数据变形，数据不平衡，特征工程（特征抽取和特征选择）

模型的选择可以根据这里来走一遍。

KNN

起初是一种分类方法，需要计算一个庞大的实例之间两两距离的矩阵，优化可以用kd-tree来做，通过把整个输入空间划分成很多很多小子区域，然后根据临近的原则把它们组织为树形结构。这样在搜索最近K个点的时候就不用全盘比较而只要比较临近几个子区域的训练数据就行了。

后来后续很多降维的方法都是基于KNN进行的。

流形学习

假设数据是均匀采样于一个高维欧氏空间中的低维流形，流形学习就是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质，找到产生数据的内在规律。根据具体方法的特性，底下又有很多分支。

T-SNE

一般用于可视化，去观察猜测数据中可能存在的一些规律和联系

它是一种非线性降维度的方法，特别适合降至二到三维的可视化

高维数据每个数据点被认为服从一种正态分布数据，低维数据同样，然后让高维数据和低维数据相似度最大。又因为t分布好算而且和正态分布逼近，所以用了t分布来算就成了tsne方法。（SNE是stochastic neighbor embedding ）

SNE改变了MDS和ISOMAP中基于距离不变的思想，将高维映射到低维的同时，尽量保证相互之间的分布概率不变，SNE将高维和低维中的样本分布都看作高斯分布，后来又出现了一个对称SNE，即让概率分布对称从而简化了运算。而T-SNE将低维中的坐标当做T分布，这样做的好处是为了让距离大的簇之间距离拉大，还能进一步解决拥挤问题。

python的sklearn有相应的实现，但是速度有些慢，所以可以线性降维之后再用进行T-SNE。tensorflow也能实现这个算法，同时如果用GPU加速的话能进一步提速。

UMAP（Uniform Manifold Approximation and Projection）

TSNE能避免集群表示的过度拥挤，在重叠区域上能表示出不同的集群。但它的局限性体现在丢失大规模信息(集群间关系)、计算时间较慢以及无法有效地表示非常大的数据集。

UMAP是建立在黎曼几何和代数拓扑理论框架上的。UMAP是一种非常有效的可视化和可伸缩降维算法。在可视化质量方面，UMAP算法与t-SNE具有竞争优势，但是它保留了更多全局结构、具有优越的运行性能、更好的可扩展性。此外，UMAP对嵌入维数没有计算限制，这使得它可以作为机器学习的通用维数约简技术

我们为什么要降维？

维度灾难，训练集的维度越高，我们就越容易过拟合，而且所需要保证效果的数据量也爆炸上升，而这是机器学习不愿意看到的。

为了减少数据的维度，要么进行特征选择，要么就是进行降维，这样可以加快后续算法，去噪去冗余，压缩数据。

降维主流有两根线，一条是投影，通过矩阵分解办法进行，一般是线性的，代表方法是PCA，LDA，NMF

一条是流形学习，一般是非线性的，考虑低维流形在高维中会弯曲，代表方法有KPCA，LLE等。

如何去衡量降维算法的表现，一种方法是反向变换算重建误差，但并不是所有的降维算法都有逆变换，最直观的方法就是观察他是不是没有丢失太多对结果有影响的信息。部分场景中可以进行串联这些方法来得到更好的效果。

这里可以快速看一下各个方法的结果大概长什么样子。

特征选择的流程

  1. 缺失值比率（missing value ratio）统计一下每个变量中的缺失值占比
  2. 低方差滤波（Low Variance Filter）归一化，去掉低方差
  3. 高相关滤波（High Correlation filter）删除携带相同信息的特征
  4. 随机森林（Random Forest）是一种自动计算特征重要性的选择方法
  5. 反向特征消除（Backward Feature Elimination）先用所有特征训练模型，评估他的性能，然后依次去掉一个特征进行模型训练，找到对模型影响最小的那个特征，删除，然后repeat
  6. 前向特征选择（Forward Feature Selection）类比反向，这次是增量的过程
  7. 因子分析（Factor Analysis）将变量按其相关性分组，即特定组内所有变量的相关性较高，组间变量的相关性较低

Graph Laplacian

就是在图论中频繁用到laplacian矩阵的一类问题

连通分量：社交网络是一个无向图，假设用户是点，关系是边，Graph Laplacian可以用来找到里面的连通分量。先构建一个邻接矩阵W，再构建一个度矩阵D，即对角线上放该节点的度（邻居个数）。定义L = D - W。L值为 0 的 eigenvalue 的个数就是 connected component 的个数。

最小割：对 L 做SVD 分解,找出 second smallest eigenvalue，设为 threshold，比它大的 entries 分到 A 类,比它小的 entries 分到 B 类。如果要割三部分，就设两个阈值。

上述具体的证明自行google。

有一种降维方法，拉普拉斯特征映射（LE）就是基于这个进行的。先把样本用KNN或者R半径的球划分的方法构建邻居图，然后用一个高斯函数计算权重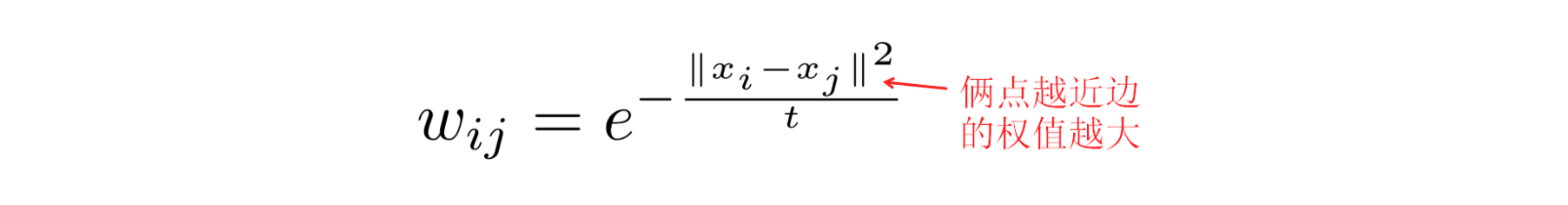权重公式

  1. 构造L
  2. 把 L 做SVD分解
  3. 找 出 top k+1 最小的 eigenvalue, 去掉为 0 的那个, 就能得到对应的 k 个维度为 （1，N）的向量, 变换成 N 个（1，k）的向量就是降维之后的点

原理是把一个图切成高内聚,低耦合的一个个块, 所以如果数据在原空间里团在一起, 他们所对应的eigenvector的取值也会很类似, 所以到了低维空间里面他们还是团在一起的。这就是我 们想要保留的聚类特性。

Kernel PCA

补充一点核技巧的知识，它可以把低维的特征映射到高维

公式

其中，RBF核可以映射到无穷维。但是我们在计算内积的时候又不用在无穷维上计算。

核PCA就是基于这个trick进行的：

  1. 利用 kernel tricks 计算 kernel matrix K = $XX^T$
  2. 对K做SVD分解,找到top k的特征向量
  3. 把高维数据 x 投射到 k 个特征向量上,从而把它降低到 k 维

需要注意的是，假设数据矩阵为X（n,m），PCA是对$X^TX$做SVD分解，这个协方差矩阵的维度是（m,m）。而KPCA的做法是对K（n，n）做SVD。

ICA（独立成分分析）

ICA又称盲源分离(Blind source separation, BSS)，长得和PCA很像，但它是用来帮助从多个维度分离有用数据的过程。PCA是ICA的数据预处理的一部分。 PCA认为主元之间彼此正交，样本呈高斯分布；ICA则不要求样本呈高斯分布。

Tensorflow的源码编译问题

安装完tensorflow之后出现

Your CPU supports instructions that this TensorFlow binary was not compiled to use: AVX2 FMA

苹果的CPU比一般的CPU更加强大，他支持AVX（高级矢量拓展）。所以为了充分发挥苹果CPU的作用，可以从源编译Tensorflow。

差异表达分析

寻找差异表达的方法：

提炼出时间序列的单细胞数据分析的一般流程

上世纪50年代，胚胎发育生物学家Conrad Hal Waddington提出的发育景观假说认为，分化成熟的细胞变回多能干细胞是个不可能发生的事件。但是日本京都大学教授山中伸弥于2006年却发现并验证，这种细胞可以发育成为身体各种组织细胞。iPS细胞的发现成就了目前轰轰烈烈的干细胞研究领域，山中伸弥教授也因此获得2012年诺贝尔生理或医学奖。

iPS (诱导多潜能干细胞)重编程实验的涌现使人们重新重视了上个世纪50年代胚胎发育生物学家Waddington提出的发育景观。虽然它只是一个隐喻,但其形象地描述了细胞的自发的层次分叉过程并隐含了细胞类型之间转换的可能性,从而作为一个整体框架最近被广泛应用来解释细胞发育和重编程。

知乎里有一篇详细文章的说明

10X表达数据 -> CellRanger -> R包Seurat-MeanVarPlot(滤掉在所有细胞表达没什么变化的基因) -> R包destiny-diffusion component embedding（降维）-> 分析维度，找到显著富集到发育过程的维度 -> R包FNN（fast-KNN）-> ForceAtlas2 （force-directed layout on KNN graph）-> Louvain-Jaccard community detection（聚类） -> Optimal Transport 算法(OT) -> 基因调控网络和基因表达模块分析 -> 其他算法比较